Пример №29 из задания 3

Два друга Юра и Ваня задумались о том, как рассчитать площадь поверхности зонта.

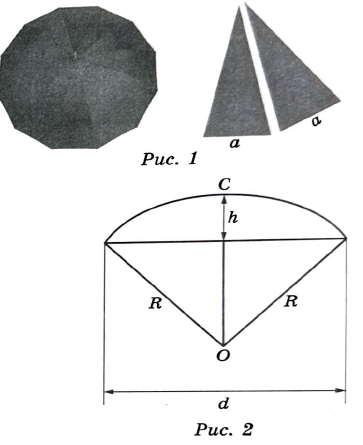
На первый взгляд зонт кажется круглым, а его купол напоминает часть сферы (сферический сегмент). Но если присмотреться, то видно, что купол зонта состоит из десяти отдельных клиньев, натянутых на каркас из десяти спиц (рис. 1). Сферическая форма в раскрытом состоянии достигается за счёт гибкости спиц и эластичности ткани, из которой изготовлен зонт.

Юра и Ваня сумели измерить расстояние между концами соседних спиц а. Оно оказалось равно 34 см. Высота купола зонта h (рис. 2) оказалась равна 25 см, а расстояние d между концами спиц, образующих дугу окружности, проходящей через вершину зонта, – ровно 110 см.

Задание 3: Ваня предложил, что купол зонта имеет форму сферического сегмента. Вычислите радиус R сферы купола, зная, что OC=R (рис. 2). Ответ дайте в сантиметрах.

Решение

Введем обозначения:

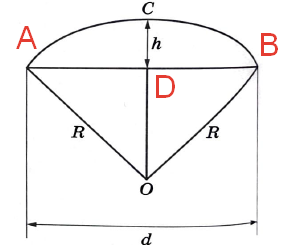
Треугольник $AOB$ – равнобедренный, т.к. $AO=BO=R$ . Значит, углы при основании равны $\angle OAD = \angle OBD$ .

$OC$ является медианой, т.к. данный отрезок является основной осью зонта и проводится ровно в центр купола. Значит, $OB$ является медианой, высотой и биссектрисой. Значит, $\angle ADO=\angle BDO=90^{\circ}$ .

Получается, что треугольник $ADO$ равен треугольнику $BDO$ по гипотенузе и острому углу.

Рассмотрим прямоугольный треугольник $ADO$ . Найдем длину $AD$ , она равняется половине расстояния $d$ :

$\displaystyle AD=\frac{d}{2}=\frac{110}{2}=55.$

Найдем $OC$ :

$OD=OC-h=R-25.$

Найдем $OA$ по теореме Пифагора:

$AO^2=AD^2+OD^2;$

$R^2=55^2+(R-25)^2;$

$R^2=3025+R^2-50R+625;$

$50R=3650;$

$R=73.$

Получилось, что радиус сферы купола равен $73$ см.