Пример №41 из задания 17

Периметр ромба равен 48, а один из углов равен 30°. Найдите площадь этого ромба.

Решение

Площадь ромба находится по формуле $\displaystyle S=a \cdot h$ , где $a$ – длина стороны ромба, $h$ – высота.

Введем обозначения:

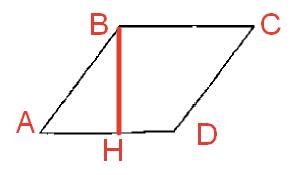
Периметр ромба равен $48$ , значит сторона ромба равна $48 \div 4 = 12$ .

Рассмотрим прямоугольный треугольник $ABH$ . Мы знаем, что в прямоугольном треугольнике катет, лежащий напротив угла $30^{\circ}$ , равен половине гипотенузы. В нашем случае $sin A=30^{\circ}$ и гипотенуза $AB=a=12$ . Значит, высота $\displaystyle BH=h=\frac{1}{2} \cdot AB=\frac{1}{2} \cdot 12=6$ .

Подставим известные значения в формулу и найдём площадь ромба:

$S=12 \cdot 6=72.$

Ответ: $72$ .

Источник: ОГЭ 2025. Математика. 50 вариантов. Типовые варианты экзаменационных заданий от разработчиков ОГЭ. Ященко И. В. (вариант 4)