Пример №17 из задания 23

Отрезки AB и CD являются хордами окружности. Найдите длину хорды CD, если AB = 18, а расстояния от центра окружности до хорд AB и CD равны соответственно 12 и 9.

Решение

Нарисуем условие и проведем отрезки $OB$ и $OC$ :

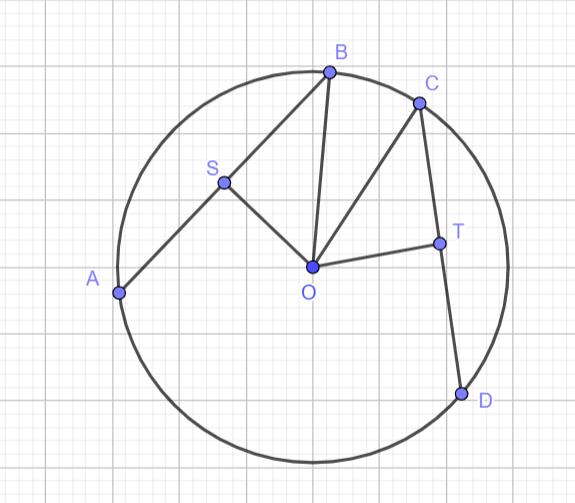
Расстоянием от центра окружности до хорд является длина перпендикуляра, т.е. $OS \perp AB$ и $OT \perp CD$ . Точки $S$ и $T$ делят хорду пополам (по свойству хорды: если радиус делит хорду пополам, то он ей перпендикулярен).

Значит, треугольники $BSO$ и $CTO$ являются прямоугольными. В них известны $BS=AB \div 2=18 \div 2=9$ и $CT=\displaystyle \frac{CD}{2}$ .

Рассмотрим прямоугольный треугольник $BSO$ и найдём гипотенузу $BO$ по теореме Пифагора:

$BO^2=OS^2+BS^2;$

$BO^2=12^2+9^2;$

$BO^2=144+81;$

$BO^2=225;$

$BO=15.$

$BO=CO=15$ – т.к. являются радиусами окружности.

Рассмотрим прямоугольный треугольник $CTO$ и найдём неизвестный катет $CT$ по теореме Пифагора:

$CO^2=OT^2+CT^2;$

$15^2=9^2+CT^2;$

$225=81+CT^2;$