Пример №38 из задания 3

Через точку, лежащую на высоте прямого кругового конуса и делящую её в отношении 1 : 2, считая от вершины конуса, проведена плоскость, параллельная его основанию и делящая конус на две части. Каков объём той части конуса, которая примыкает к его основанию, если объём всего конуса равен 54?

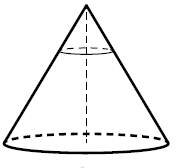
Решение

Объем конуса находится по формуле $\displaystyle V=\frac{1}{3} \pi R^2 h$ , где $R$ – радиус основания, $h$ – высота конуса.

Всего конус разделен на $2+1=3$ части. Радиус и высота отсеченного конуса в $3$ раза меньше.

Найдем объем отсеченного конуса $\displaystyle V_2=\frac{1}{3} \pi (\frac{1}{3}R)^2 \frac{1}{3}h=\frac{1}{27} \cdot \frac{1}{3} \pi R^2 h=\frac{1}{27} \cdot V_1=\frac{1}{27} \cdot 54=2$ .

Найдем объем той части конуса, которая примыкает к его основанию $V=54-2=52$ .

Ответ: $52$ .

Источник: Демоверсия ЕГЭ по математике 2024. Профильный уровень (Задание 3. Пример 2)