Пример №17 из задания 16

Радиус окружности, описанной около квадрата, равен $24\sqrt{2}$ . Найдите радиус окружности, вписанной в этот квадрат.

Решение

Нарисуем радиусы:

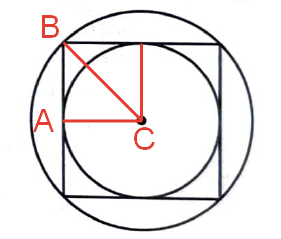
$AC$ равен радиусу вписанной окружности.

Из прямоугольного треугольника $ABC$ найдем сторону $AC$ по теореме Пифагора:

$BC^2=AB^2+AC^2;$

$(24\sqrt{2})^2=AB^2+AC^2;$

$AC=AB=r$ , значит:

$576 \cdot 2=r^2+r^2;$

$1152=2r^2;$

$r^2=576;$

$r=24.$

Получилось, что радиус вписанной окружности равен $24.$

Ответ: $24$ .

Источник: ОГЭ-2025. Математика. Типовые экзаменационные варианты. 36 вариантов. Ященко И. В. (вариант 26)

ОГЭ-2024. Математика. Типовые экзаменационные варианты. 36 вариантов (вариант 16)

0 0 голоса

Рейтинг статьи

0 комментариев

Старые

Новые Популярные

Межтекстовые Отзывы

Посмотреть все комментарии