Пример №30 из задания 17

Диагонали AC и BD трапеции ABCD с основания BC и AD пересекаются в точке O, BC=4, AD=9, AC=26. Найдите AO.

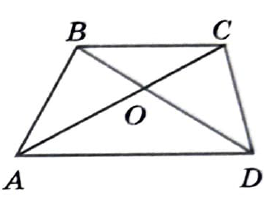
Решение

Треугольники $AOD$ и $BOC$ подобны по первому признаку подобия – если два угла одного треугольника соответственно равны двум углам другого:

$\angle AOD=\angle BOC$ как вертикальные углы;

$\angle DAO=\angle BCO$ как накрест лежащие углы при параллельных прямых ( $BCD$ параллельна $AD$ , т.к. $ABCD$ трапеция) и секущей $AC$ .

У подобных треугольников соответственные стороны пропорциональны. Значит, можно записать:

Найдем $CO=AC-AO=26-AO.$

$\displaystyle \frac{AD}{BC}=\frac{AO}{CO};$

$\displaystyle \frac{9}{4}=\frac{AO}{CO}.$

Отсюда:

$\displaystyle \frac{9}{4}=\frac{AO}{26-AO};$

$4AO=9 \cdot (26-AO);$

$4AO=234-9AO;$

$4AO+9AO=234;$

$13AO=494;$

$AO=18.$

Ответ: $18$ .

Источник: ОГЭ-2024. Математика. Типовые экзаменационные варианты. 36 вариантов (вариант 30)

0 0 голоса

Рейтинг статьи

0 комментариев

Старые

Новые Популярные

Межтекстовые Отзывы

Посмотреть все комментарии