Пример №382 из задания 2
В прямоугольном треугольнике ABC катет AC равен \sqrt{3}. Найдите скалярное произведение \overrightarrow{AB} \cdot \overrightarrow{AC}
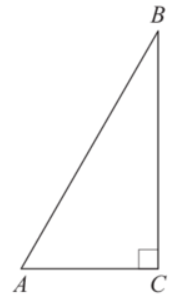
Решение
Скалярное произведение векторов равняется произведению их длин на косинус угла между ними:
\overrightarrow{AB} \cdot \overrightarrow{AC} = \overrightarrow{|AB|} \cdot \overrightarrow{|AC|} \cdot \cos A.
Косинус – отношение прилежащего катета к гипотенузе:
\displaystyle cos A=\frac{AC}{AB}.
Отсюда:
\displaystyle \overrightarrow{AB} \cdot \overrightarrow{AC} = \overrightarrow{|AB|} \cdot \overrightarrow{|AC|} \cdot \frac{\overrightarrow{|AC|}}{\overrightarrow{|AB|}}=\overrightarrow{|AC|} \cdot \overrightarrow{|AC|}=\sqrt{3} \cdot \sqrt{3}=3.
Ответ: 3.
Источник: Открытый банк задач ЕГЭ по математике (Задание №509532)
Подготовка к ОГЭ по математике - что нужно знать школьнику
Алгебра в жизни - 7 примеров, где тебе пригодятся школьные знания
Как понять геометрию - визуальные методы для запоминания теорем
Почему важно задавать вопросы - как не бояться спрашивать на уроке
Готовимся к контрольной - план на неделю для 7–9 классов
Квадратные уравнения. Решение квадратных уравнений. Дискриминант. Формула дискриминанта. Примеры.
Подписаться
авторизуйтесь
0 комментариев
Старые
