Пример №31 из задания 2
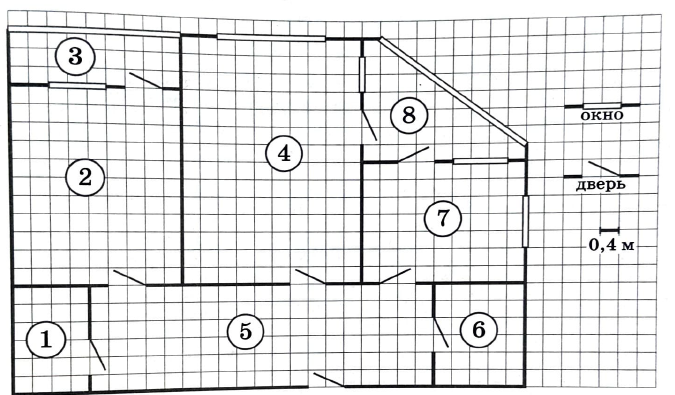
На рисунке изображён план двухкомнатной квартиры в многоэтажном жилом доме. В правой части рисунка даны обозначения двери и окна, а также указано, что длина стороны клетки на плане соответствует 0,4 м. Вход в квартиру находится в прихожей. Справа от входа в квартиру располагаются кухня и санузел, а также одна из лоджий, в которую можно попасть из кухни. В эту же лоджию можно пройти и из гостиной. Наименьшую площадь имеет кладовая. В квартире есть ещё одна лоджия, куда можно попасть из прихожей, пройдя через спальню.
Задание 2: Найдите ширину остекления в той лоджии, которая примыкает к кухне. Ответ дайте в метрах.
Решение
Из задания 1 известно, что лоджия которая примыкает к кухня обозначена номером 8.
Введем обозначения:
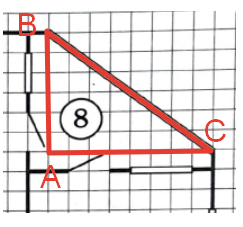
Рассмотри прямоугольный треугольник ABC где необходимо найти ширину остекления, т.е. сторону BC.
Известно (по изображению), что AB=6 клеток и AC=8 клеток. Найдем гипотенузу BC по теореме Пифагора:
BC^2=AB^2+AC^2;
BC^2=8^2+6^2;
BC^2=64+36;
BC^2=100;
BC=10 клеток.
По условию известно, что длина стороны клетки на плане соответствует 0,4 м.
Найдем ширину остекления в метрах:
10 \cdot 0,4=4 м.
Ответ: 4.
Источник: ОГЭ-2025. Математика. Типовые экзаменационные варианты. 36 вариантов. Ященко И. В. (вариант 26)
ОГЭ-2024. Математика. Типовые экзаменационные варианты. 36 вариантов (вариант 16)
Алгебра в жизни - 7 примеров, где тебе пригодятся школьные знания
Интерактивные способы учить математику - сайты, приложения, игры
Квадратные уравнения. Решение квадратных уравнений. Дискриминант. Формула дискриминанта. Примеры.
Готовимся к контрольной - план на неделю для 7–9 классов
Почему важно задавать вопросы - как не бояться спрашивать на уроке
Как понять геометрию - визуальные методы для запоминания теорем
Подписаться
авторизуйтесь
0 комментариев
Старые
