Пример №18 из задания 20

Решите неравенство $\displaystyle -\frac{17}{x^2-2x-24} \leq 0.$

Решение

ОДЗ:

$x^2-2x-24 \neq 0;$

$D=b^2-4ac=4-4 \cdot 1 \cdot (-24)=100;$

$\displaystyle x_1=\frac{-b+\sqrt{D}}{2a}=\frac{2+10}{2}=6;$

$\displaystyle x_2=\frac{-b-\sqrt{D}}{2a}=\frac{2-10}{2}=-4.$

Получилось, что $x \neq 6$ и $x \neq -4.$

Неравенство не может быть равно нулю, т.к. числитель не равен нулю.

Т.к. числитель отрицательное число, то неравенство будет меньше нуля, если знаменатель будет больше нуля, т.е. $x^2-2x-24>0 .$

Воспользуемся методом интервалов:

$x^2-2x-24=0;$

$x_1=6;$

$x_2=-4.$

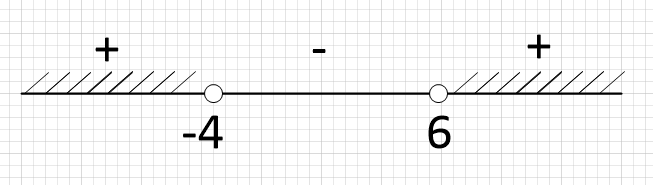
Получилось, что $x \in (-\infty; 4) \cup (6; +\infty).$

Ответ: $x \in (-\infty; 4) \cup (6; +\infty).$

Источник: ОГЭ-2025. Математика. Типовые экзаменационные варианты. 36 вариантов. Ященко И. В. (вариант 27)

ОГЭ-2024. Математика. Типовые экзаменационные варианты. 36 вариантов (вариант 17)

0 0 голоса

Рейтинг статьи

0 комментариев

Старые

Новые Популярные

Межтекстовые Отзывы

Посмотреть все комментарии