Пример №4 из задания 7

На рисунке изображены график функции и касательные, проведённые к нему в точках с абсциссами A, B, C и D.

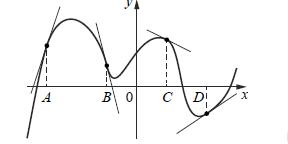
В правом столбце указаны значения производной функции в точках A, B, C и D. Пользуясь графиком, поставьте в соответствие каждой точке значение производной функции в ней.

Решение

Если касательная образует острый угол с осью X, то она положительная. Если касательная образуется тупой угол с осью X, то она отрицательная. Причем, чем больше угловой коэффициент касательно, тем больше значение (по модулю) принимает производная.

Разберем каждую точку:

Точка А: Касательная образует острый угол и имеет один из наибольших угловых коэффициентов. Значит производная положительная и максимальная. Подходит ответ под номером 2.

Точка B: Касательная образует тупой угол и имеет один из наибольших угловых коэффициентов. Значит производная отрицательная и максимальная. Подходит ответ под номером 1.

Точка C: Касательная образует тупой угол и имеет меньший угловой коэффициент чем у точки B. Подходит ответ под номером 4.

Точка D: Касательная образует острый угол и имеет меньший угловой коэффициент чем у точки A. Подходит ответ под номером 3.

Получилась следующая последовательность 2143.

Ответ: 2143.

Источник: ЕГЭ 2025. Демоверсия (задание 7.1)