Пример №41 из задания 15

Сторона равностороннего треугольника равна $16\sqrt{3}$ . Найдите высоту этого треугольника.

Решение

Введем обозначения:

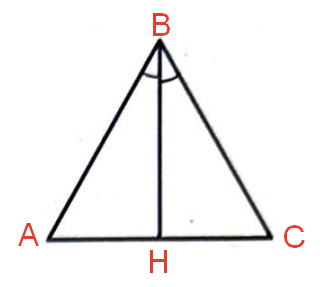
Треугольник $ABC$ – равносторонний. А в равностороннем треугольнике высота, проведенная к основанию, является медианой и биссектрисой.

А медиана делит сторону пополам на которую она опущена. Значит сторона:

$\displaystyle AH=HC=\frac{AC}{2}=\frac{16\sqrt{3}}{2}=8\sqrt{3}.$

Треугольник $ABH$ является прямоугольным, т.к. $BH$ – высота. По теореме Пифагора из прямоугольного треугольника $ABH$ найдем высоту $BH:$

$AB^2=AH^2+BH^2;$

$(16\sqrt{3})^2=(8\sqrt{3})^2+BH^2;$

$256 \cdot 3=64 \cdot 3+BH^2;$

$768-192=BH^2;$

$BH^2=576;$

$BH=24.$

Получилось, что высота треугольника равна $24$ .

Ответ: $24$ .

Источник: ОГЭ 2025. Математика. 50 вариантов. Типовые варианты экзаменационных заданий от разработчиков ОГЭ. Ященко И. В. (вариант 4)

0 0 голоса

Рейтинг статьи

0 комментариев

Старые

Новые Популярные

Межтекстовые Отзывы

Посмотреть все комментарии