Пример №55 из задания 15

На стороне AC треугольника ABC отмечена точка D так, что AD=2, DC=13. Площадь треугольника ABC равна 75. Найдите площадь треугольника ABD.

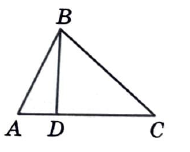
Решение

Воспользуемся формулой $\displaystyle S=\frac{1}{2} \cdot a \cdot h$ , где $a$ – длина основания, $h$ – высота, проведенная к основанию.

Найдем основание $AC=AD+DC=2+13=15$ .

Проведем высоту:

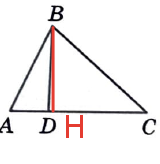
Мы знаем площадь треугольника $ABC$ и основание $AC$ . Найдем высоту $BH$ , проведенную к основанию:

$\displaystyle S_{ABC}=\frac{1}{2} \cdot AC \cdot BH;$

$\displaystyle 75=\frac{1}{2} \cdot 15 \cdot BH;$

$75=7,5 \cdot BH;$

$BH=10.$

Высота $BH$ является высотой как для треугольника $ABC$ , так и для треугольника $ABD$ .

Найдем площадь треугольника $ABD$ по формуле $\displaystyle S=\frac{1}{2} \cdot a \cdot h.$

$\displaystyle S_{ABD}=\frac{1}{2} \cdot AD \cdot BH;$

$\displaystyle S_{ABD}=\frac{1}{2} \cdot 2 \cdot 10=10.$

Ответ: $10$ .

Источник: ОГЭ 2025. Математика. 50 вариантов. Типовые варианты экзаменационных заданий от разработчиков ОГЭ. Ященко И. В. (вариант 20)

0 0 голоса

Рейтинг статьи

0 комментариев

Старые

Новые Популярные

Межтекстовые Отзывы

Посмотреть все комментарии