Пример №50 из задания 16

На окружности с центром О отмечены точки A и B так, что ∠AOB=120°. Длина меньшей дуги АВ равна 67. Найдите длину большей дуги AB.

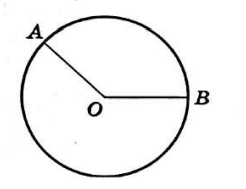
Решение

Градусная мера меньшей дуги (угол $AOB$ ) равна длине меньшей дуги, значит, одна единица длины меньшей дуги равна $\displaystyle 120\div 67=\frac{120}{67}^{\circ}$ .

Весь круг равен $360^{\circ}$ , а градусная мера большей дуги равна $360-120=240^{\circ}$ . Значит, длина дуги равна $\displaystyle 240\div \frac{120}{67}=134^{\circ}$ .

Ответ: $134$ .

Источник: ОГЭ 2025. Математика. 50 вариантов. Типовые варианты экзаменационных заданий от разработчиков ОГЭ. Ященко И. В. (вариант 14)