Пример №83 из задания 15

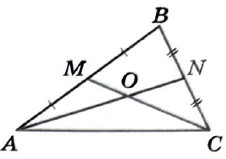
Точка M и N является серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN и CM пересекаются в точке O, AN=27, CM=9. Найдите AO.

Решение

$AN$ и $CM$ является медианами, т.к. точки $M$ и $N$ являются серединами сторон $AB$ и $BC$ .

Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении $2:1$ , считая от вершины.

Значит, медиана $AN$ делится на отрезки в отношении $AO=2$ и $ON=1$ . А всего медиана имеет $AN=AO+ON=2+1=3$ части.

Найдем какой длины одна часть $27 \div 3=9$ . А отрезок $AO$ имеет две части, значит, данный отрезок $AO=9 \cdot 2 = 18$ .

Ответ: $18$ .

Источник: ОГЭ 2025. Математика. 50 вариантов. Типовые варианты экзаменационных заданий от разработчиков ОГЭ. Ященко И. В. (вариант 44)

0 0 голоса

Рейтинг статьи

0 комментариев

Старые

Новые Популярные

Межтекстовые Отзывы

Посмотреть все комментарии