Пример №61 из задания 20

Решите неравенство $(x-5)^2<\sqrt{7}(x-5).$

Решение

$(x-5)^2<\sqrt{7}(x-5);$

$(x-5)^2-\sqrt{7}(x-5)<0;$

$(x-5)((x-5)-\sqrt{7})<0;$

Воспользуемся методом интервалов:

$(x-5)((x-5)-\sqrt{7})=0;$

Уравнение равно нулю, если $x-5=0$ или $(x-5)-\sqrt{7}=0.$

$x-5=0;$

$x=5.$

ИЛИ

$(x-5)-\sqrt{7}=0;$

$x-5-\sqrt{7}=0;$

$x=5+\sqrt{7}.$

Изобразим решение:

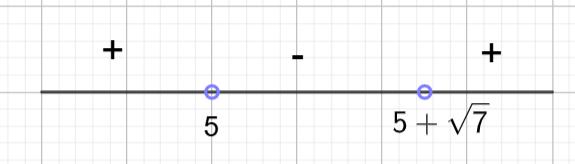
Получилось, что $x \in (5; 5+\sqrt{7})$ .

Ответ: $x \in (5; 5+\sqrt{7})$

Источник: ОГЭ 2025. Математика. 50 вариантов. Типовые варианты экзаменационных заданий от разработчиков ОГЭ. Ященко И. В. (вариант 31)

0 0 голоса

Рейтинг статьи

0 комментариев

Старые

Новые Популярные

Межтекстовые Отзывы

Посмотреть все комментарии