Пример №4 из задания 23

Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 45° и 150°, а CD = 32.

Решение

Нарисуем трапецию $ABCD$ и проведем в нем высоты $AH$ и $CE$ :

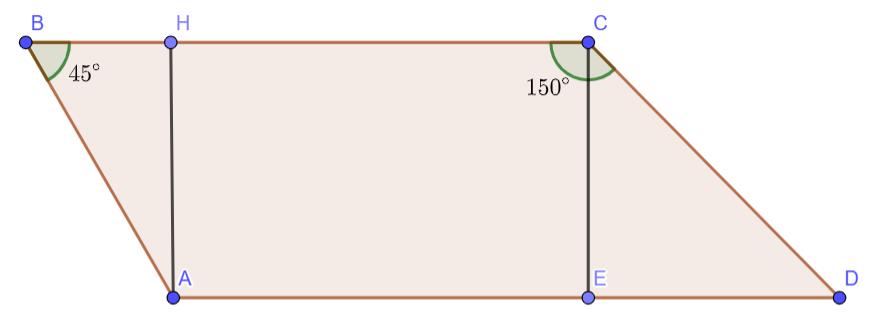
$\angle ECD=\angle BCD — \angle BCE=150^{\circ}-90^{\circ}=60^{\circ}$ .

Рассмотрим треугольник $CED$ , в котором известны углы $\angle CED=90^{\circ}; \angle DCE = 60^{\circ}; \angle EDC = 180^{\circ}-90^{\circ}-60^{\circ}=30^{\circ}$ . Мы знаем, что косинус – отношение прилежащего катета к гипотенузе. Значит, можно записать:

$\displaystyle cos \angle DCE=\frac{CE}{CD};$

$\displaystyle cos 60^{\circ}=\frac{CE}{32};$

$\displaystyle \frac{1}{2}=\frac{CE}{32};$

$2CE=32;$

$\displaystyle CE=16.$

У трапеции высоты равны, значит, $\displaystyle AH=CE=16.$

Рассмотрим прямоугольный треугольник $ABH$ , в котором известны углы $\angle AHB=90^{\circ}; \angle HBA = 45^{\circ}; \angle HAB=180^{\circ}-45^{\circ}-90^{\circ}=45^{\circ}$ . Мы знаем, что синус – отношение противолежащего катета к гипотенузе. Значит, можно записать:

$\displaystyle sin \angle HBA=\frac{AH}{AB};$

$\displaystyle sin 45^{\circ}=\frac{16}{AB};$

$\displaystyle \frac{\sqrt{2}}{2}=\frac{16}{AB};$

$\displaystyle \sqrt{2}AB=16 \cdot 2;$

$\displaystyle \sqrt{2}AB=32;$

$\displaystyle AB=\frac{32}{\sqrt{2}}=\frac{32 \cdot \sqrt{2}}{\sqrt{2} \cdot \sqrt{2}}=\frac{32\sqrt{2}}{2}=16\sqrt{2}$ .

Ответ: $16\sqrt{2}$ .

Источник: ОГЭ 2025. Математика. 50 вариантов. Типовые варианты экзаменационных заданий от разработчиков ОГЭ. Ященко И. В. (вариант 3)