Пример №6 из задания 23

Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M. Найдите MC, если AB = 15, DC = 30, AC = 39.

Решение

Нарисуем условие:

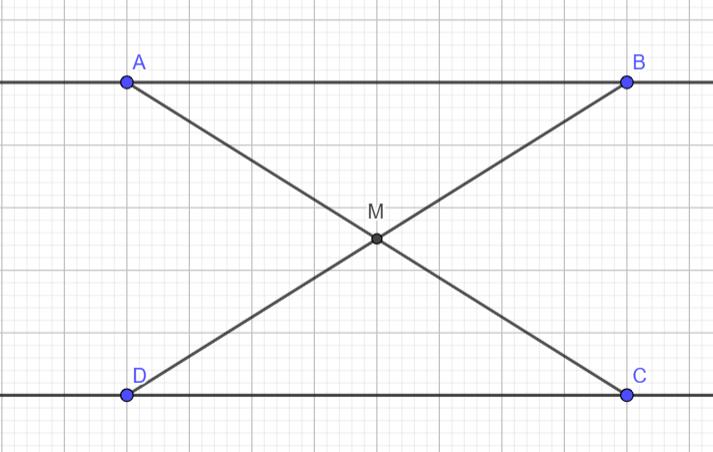
Треугольник $ABM$ подобен треугольнику $CDM$ по двум углам:

– $\angle AMB=\angle DMC$ – как вертикальные углы;

– $\angle ABD=\angle CDB$ – как накрест лежащие углы при параллельных прямых $AB$ и $CD$ и секущей $BD$ .

У подобных треугольников стороны пропорциональны:

$\displaystyle \frac{AB}{CD}=\frac{AM}{CM}=\frac{BM}{DM}.$

Пусть $CM=x$ . Тогда $AM=AC-CM=39-x$ .

Подставим значения в соотношение:

$\displaystyle \frac{AB}{CD}=\frac{AM}{CM};$

$\displaystyle \frac{15}{30}=\frac{39-x}{x};$

$15x=30(39-x);$

$15x=1170-30x;$

$45x=1170;$

$x=26.$

Ответ: $26$ .

Источник: ОГЭ 2025. Математика. 50 вариантов. Типовые варианты экзаменационных заданий от разработчиков ОГЭ. Ященко И. В. (вариант 5)

0 0 голоса

Рейтинг статьи

0 комментариев

Старые

Новые Популярные

Межтекстовые Отзывы

Посмотреть все комментарии