Пример №14 из задания 23

Прямая, параллельная основаниям трапеции ABCD, пересекает ее боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD = 35, BC = 21, CF : DF = 5 : 2.

Решение

Нарисуем условие и проведем диагональ $BD$ :

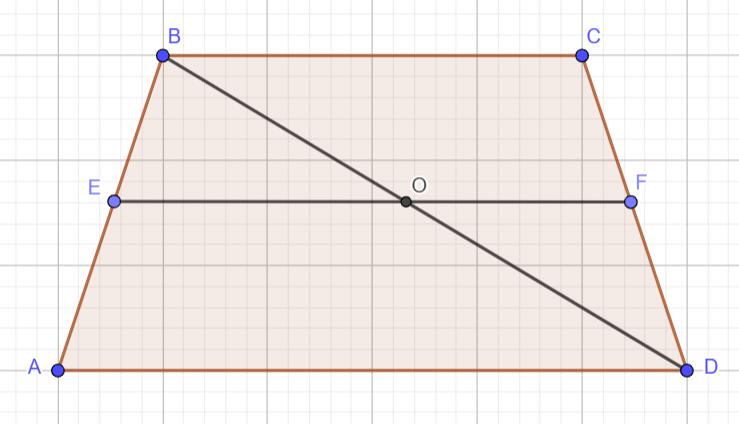
Теорема Фалеса гласит: Параллельные прямые, пересекающие стороны угла, отсекают от его сторон пропорциональные отрезки. Можно записать:

$\displaystyle \frac{BE}{AE}=\frac{CF}{FD}=\frac{5}{2}$ .

Треугольник $BCD$ подобен треугольнику $OFD$ по двум углам:

– $\angle BDC$ общий;

– $\angle BCD=\angle OFD$ как соответственные углы.

У подобных треугольников стороны пропорциональны:

$\displaystyle \frac{BC}{OF}=\frac{CD}{DF}$ .

$\displaystyle \frac{CD}{DF}=\frac{CF+DF}{DF}=\frac{CF}{DF}+1=\frac{5}{2}+1=\frac{7}{2}$ .

Можно записать:

$\displaystyle \frac{BC}{OF}=\frac{7}{2};$

$\displaystyle \frac{21}{OF}=\frac{7}{2};$

$\displaystyle 7OF=42;$

$\displaystyle OF=6.$

Треугольник $ABD$ подобен треугольнику $EBO$ по двум углам:

– $\angle ABD$ общий;

– $\angle BAD=\angle BEO$ как соответственные углы.

У подобных треугольников стороны пропорциональны:

$\displaystyle \frac{AD}{EO}=\frac{AB}{BE}$ .

$\displaystyle \frac{AB}{BE}=\frac{AE+BE}{BE}=\frac{AE}{BE}+1=\frac{2}{5}+1=\frac{7}{5}$ .

Можно записать:

$\displaystyle \frac{AD}{EO}=\frac{7}{5};$

$\displaystyle \frac{35}{EO}=\frac{7}{5};$

$\displaystyle 7EO=175;$

$\displaystyle EO=25.$

Найдем длину отрезка $EF=EO+OF=25+6=31.$

Ответ: $31$ .

Источник: ОГЭ 2025. Математика. 50 вариантов. Типовые варианты экзаменационных заданий от разработчиков ОГЭ. Ященко И. В. (вариант 13)

0 0 голоса

Рейтинг статьи

0 комментариев

Старые

Новые Популярные

Межтекстовые Отзывы

Посмотреть все комментарии

Пример №14 из задания 23

Решение

Интересные статьи: