Пример №26 из задания 23

Биссектриса угла A параллелограмма ABCD пересекает сторону BC в точке K Найдите периметр параллелограмма, если BK = 4, CK = 19.

Решение

Нарисуем условие:

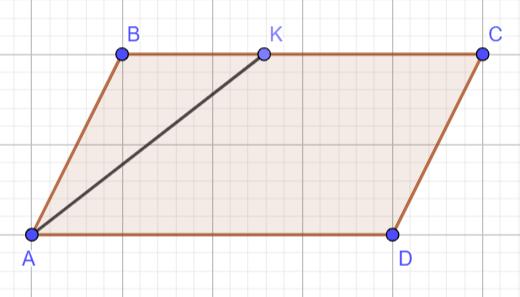
У параллелограмма противоположные стороны параллельны. Поэтому $\angle BKA=\angle DAK$ – как накрест лежащие углы при параллельных прямых $BC$ и $AD$ и секущей $AK$ .

Биссектриса делит угол пополам. Поэтому $\angle BAK=\angle DAK$ .

С условием выше можно написать, что $\angle BAK=\angle DAK=\angle BKA$ . Отсюда получается, что треугольника $ABK$ является равнобедренным. Значит, $AB=BK=4$ .

У параллелограмма противоположные стороны равны, поэтому:

$AB=DC=4;$

$AD=BC=BK+KC=4+19=23.$

Найдём периметр параллелограмма:

$P=4+23+4+23=54.$

Ответ: $54$ .

Источник: ОГЭ 2025. Математика. 50 вариантов. Типовые варианты экзаменационных заданий от разработчиков ОГЭ. Ященко И. В. (вариант 25)