Пример №30 из задания 23

Катет и гипотенуза прямоугольного треугольника равны 8 и 17 соответственно. Найдите высоту, проведённую к гипотенузе.

Решение

Нарисуем условие:

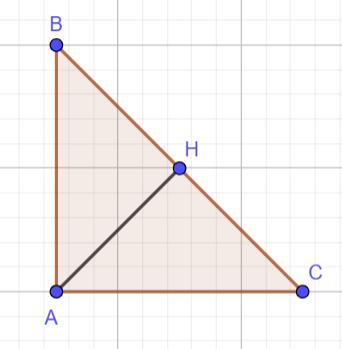
Найдём чему равен неизвестный катет $BC$ по теореме Пифагора:

$BC^2=AB^2+AC^2;$

$17^2=8^2+AC^2;$

$289=64+AC^2;$

$AC^2=225;$

$AC=15.$

Площадь прямоугольного треугольника равна половине произведения его катетов $\displaystyle S=\frac{a \cdot b}{2}=\frac{AB \cdot AC}{2}=\frac{8 \cdot 15}{2}=60.$

Высоту можно найти из площади прямоугольного треугольника $\displaystyle S=\frac{a \cdot h}{2}=\frac{BC \cdot AH}{2}$ .

Подставим известные данные в формулу и найдём высоту:

$\displaystyle S=\frac{BC \cdot AH}{2};$

$\displaystyle 60=\frac{17 \cdot AH}{2};$

$120=17AH;$

$\displaystyle AH=\frac{120}{17}.$

Ответ: $\displaystyle \frac{120}{17}$ .

Источник: ОГЭ 2025. Математика. 50 вариантов. Типовые варианты экзаменационных заданий от разработчиков ОГЭ. Ященко И. В. (вариант 29)

0 0 голоса

Рейтинг статьи

0 комментариев

Старые

Новые Популярные

Межтекстовые Отзывы

Посмотреть все комментарии

Пример №30 из задания 23

Решение

Интересные статьи: