Пример №41 из задания 23
Диагонали AC и BD параллелограмма ABCD пересекаются в точке O. К стороне AD проведена высота BH, которая пересекает отрезок AO в точке K, причём AK : KO = 8 : 3. Найдите высота BH, если KH = 6.
Решение
Нарисуем условие и проведем высоту EF через точку пересечения диагоналей, параллельную высоте BH:
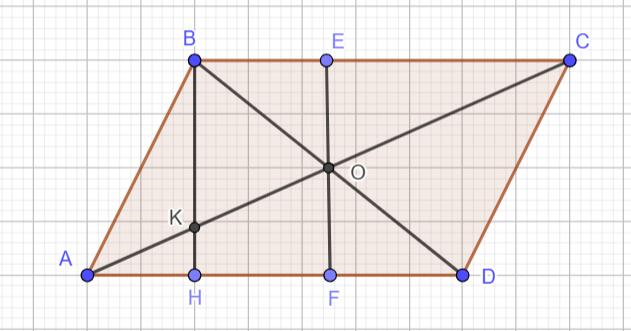
Треугольник AKH подобен треугольнику AOF по двум углам:
– \angle A – общий;
– \angle AKH=\angle AOF – как соответственные при при параллельных прямых BH и EF и секущей AC.
У подобных треугольников стороны пропорциональны:
\displaystyle \frac{AK}{AO}=\frac{KH}{OF}.
Пусть x – коэффициент пропорциональности подобных треугольников. Тогда можно написать, что AK=8x; KO=3x. Отсюда найдем AO=AK+KO=8x+3x=11x.
Подставим известные значения в формулу и найдём OF:
\displaystyle \frac{8x}{11x}=\frac{6}{OF};
66x=8x \cdot OF;
OF=8,25.
\displaystyle BH=EF=2OF=2 \cdot 8,25=16,5.
Ответ: 16,5.
Источник: ОГЭ 2025. Математика. 50 вариантов. Типовые варианты экзаменационных заданий от разработчиков ОГЭ. Ященко И. В. (вариант 40)
Интерактивные способы учить математику - сайты, приложения, игры
Как понять геометрию - визуальные методы для запоминания теорем
5 распространённых ошибок в решении уравнений и как их избежать
Почему важно задавать вопросы - как не бояться спрашивать на уроке
Готовимся к контрольной - план на неделю для 7–9 классов
Квадратные уравнения. Решение квадратных уравнений. Дискриминант. Формула дискриминанта. Примеры.
Подписаться
авторизуйтесь
0 комментариев
Старые
