Пример №3 из задания 24

Биссектрисы углов B и C параллелограмма ABCD пересекаются в точке M, лежащей на стороне AD. Докажите, что M — середина AD.

Решение

Нарисуем условие:

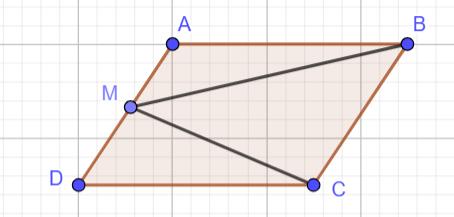
У параллелограмма противоположные стороны равны и параллельным $AB=DC; AD \parallel BC$ .

Биссектриса делит угол пополам, значит $\angle ABM=\angle CBM$ и $\angle CBM=\angle AMB$ – как внутренние накрест лежащий углы при параллельных прямых $AD$ и $BC$ и секущей $BM$ . Отсюда можно написать:

$\angle ABM=\angle CBM=\angle AMB.$

Значит, треугольник $ABM$ является равнобедренным. А у равнобедренного треугольника две стороны равны $AB=AM$ .

Биссектриса делит угол пополам, значит $\angle BCM=\angle DCM$ и $\angle BCM=\angle CMD$ – как внутренние накрест лежащий углы при параллельных прямых $AD$ и $BC$ и секущей $CM$ . Отсюда можно написать:

$\angle BCM=\angle DCM=\angle CMD.$

Значит, треугольник $DCM$ является равнобедренным. А у равнобедренного треугольника две стороны равны $MD=CD$ .

Значит $AB=AM=MD=DC$ , т.е. $AM=MD$ . Получается $M$ – середина стороны $AD$ , что и требовалось доказать.

Источник: ОГЭ 2025. Математика. 50 вариантов. Типовые варианты экзаменационных заданий от разработчиков ОГЭ. Ященко И. В. (вариант 2)