Пример №2 из задания 11

Найдите точку максимума функции $y=15+21x-4x\sqrt{x}$ .

Решение

Найдем производную функции, для этого преобразуем функцию $\displaystyle y=15+21x-4x\cdot x^{\frac{1}{2}}=15+21x-4x^{\frac{3}{2}}$ :

$\displaystyle y’=21-4\cdot\frac{3}{2}\cdot x^{\frac{1}{2}}=21-6\sqrt{x}$ .

Найдем точки экстремума функции, для этого приравняем производную функции к нулю:

$21-6\sqrt{x}=0;$

$\sqrt{x}=\frac{21}{6}=3,5;$

$x=12,25.$

Определим знаки производной функции и изобразим на рисунке поведение функции:

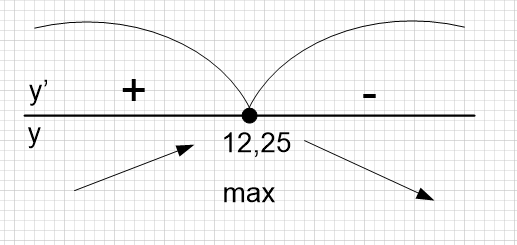
Точка максимума – точка, где производная меняет свой знак с плюса на минус. В нашем случае точка максимума $12,25$ .

Ответ: $12,25$ ,

Источник: ЕГЭ 2023 Математика. Профильный уровень. Типовые экзаменационные варианты. 36 вариантов (вариант 2) (Купить книгу)

0 0 голоса

Рейтинг статьи

0 комментариев

Старые

Новые Популярные

Межтекстовые Отзывы

Посмотреть все комментарии