Пример №10 из задания 11
Найдите наименьшее значение функции y=e^{2x}-9e^x-3 на отрезке [0; 3] .
Решение
Наименьшее значение функция принимает в одной из точек экстремума. Чтобы найти их, найдем производную функции и приравняем ее к нулю.
Найдем производную функции, для этого воспользуемся правилом дифференцирования (e^x)’=e^x \cdot x’:
y’=2e^{2x}-9e^x.
2e^{2x}-9e^x=0;
e^x(2e^x-9)=0;
e^x=0 – всегда больше нуля.
2e^x-9=0;
x=ln4,5.
Определим знаки производной функции и изобразим на рисунке поведение функции на отрезке [0;3]:
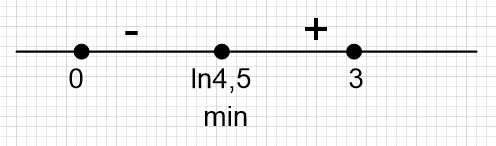
Получилось, что наименьшее значение функции в точке ln4,5. Найдем значение функции в данной точке:
\displaystyle y(ln4,5)=e^{2ln4,5}-9e^{ln4,5}-3= (e^{ln4,5})^2-9\cdot 4,5-3=4,5^2-40,5-3=-23,25.
Ответ: -23,25.
Источник: ЕГЭ 2023 Математика. Профильный уровень. Типовые экзаменационные варианты. 36 вариантов (вариант 10) (Купить книгу)










