Пример №24 из задания 11

Найдите точку минимума функции $y=(x+4)^2 (x+1)+9$ .

Решение

Для нахождения производной применим следующее правило дифференцирования $(uv)’=u’v+uv’$ :

$y’=((x+4)^2)'(x+1)+(x+4)^2(x+1)’=$ $(2x+8)(x+1)+(x^2+8x+16)=$ $2x^2+10x+8)+(x^2+8x+16)=$ $3x^2+18x+24$ .

Найдем точки экстремума функции, для этого приравняем производную функции к нулю:

$3x^2+18x+24=0;$

$D=b^2-4ac=324-4\cdot3\cdot24=36$

$\displaystyle x_1=\frac{-18+6}{6}=-2;$

$\displaystyle x_1=\frac{-18-6}{6}=-4.$

Определим знаки производной функции и изобразим на рисунке поведение функции:

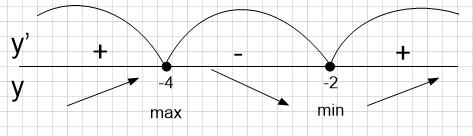
Точка минимума – точка, где производная меняет свой знак с минуса на плюс. В нашем случае точка минимума $-2$ .

Ответ: $-2$ .

Источник: ЕГЭ 2023 Математика. Профильный уровень. Типовые экзаменационные варианты. 36 вариантов (вариант 24) (Купить книгу)

0 0 голоса

Рейтинг статьи

0 комментариев

Старые

Новые Популярные

Межтекстовые Отзывы

Посмотреть все комментарии