Пример №4 из задания 12
Одна из диагоналей ромба равна 12, а его площадь равна 96. Найдите сторону ромба.
Решение
Площадь ромба находится по формуле \displaystyle S=\frac{d_1\cdot d_2}{2}, где d_1 и d_2 – диагонали ромба.
Подставим известные значения в формулу и найдем вторую диагональ ромба:
\displaystyle 96=\frac{12d_2}{2};
192=12d_2;
d_2=16.
Рассмотрим прямоугольный треугольник ABO.
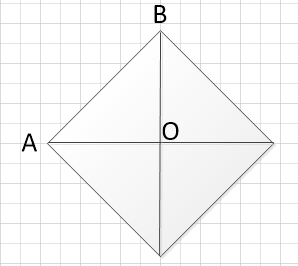
Мы знаем, что диагонали ромба точкой пересечения делятся пополам, т.е. AO=12\div 2=6 и BO=16\div 2=8. Найдем гипотенузу AB по теореме Пифагора:
AB^2=AO^2+BO^2;
AB^2=6^2+8^2;
AB=10.
Получилось, что сторона ромба равна 10.
Ответ: 10.
Источник: ЕГЭ 2023 Математика. Базовый уровень. Типовые экзаменационные варианты. 30 вариантов (вариант 5) (Купить книгу)
Как понять геометрию - визуальные методы для запоминания теорем
Готовимся к контрольной - план на неделю для 7–9 классов
Алгебра в жизни - 7 примеров, где тебе пригодятся школьные знания
Интерактивные способы учить математику - сайты, приложения, игры
Почему важно задавать вопросы - как не бояться спрашивать на уроке
5 распространённых ошибок в решении уравнений и как их избежать
Подписаться
авторизуйтесь
0 комментариев
Старые
