Пример №5 из задания 12

В ромбе $ABCD$ известно, что $AB = 5$ , $BD = 2\sqrt{21}$ . Найдите синус угла $ABD$ .

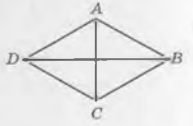
Решение

Мы знаем, что диагонали ромба точкой пересечения делятся пополам, значит $BO=2\sqrt{21}\div 2=\sqrt{21}$ .

Найдем косинус угла $ABD$ (косинус – отношение прилежащего катета к гипотенузе) из прямоугольного треугольника $ABO$ :

$\displaystyle cosABD=\frac{BO}{AB}=\frac{\sqrt{21}}{5}$ .

Для нахождения синуса угла $ABD$ воспользуемся основным тригонометрических тождеством $sin^2x+cos^2x=1$ .

$\displaystyle sin^2 ABD+\left(\frac{\sqrt{21}}{5}\right)^2=1;$

$\displaystyle sin^2 ABD=1-\frac{21}{25};$

$sin ABD=0,4$ .

Ответ: $0,4$ .

Источник: ЕГЭ 2023 Математика. Базовый уровень. Типовые экзаменационные варианты. 30 вариантов (вариант 6) (Купить книгу)

0 0 голоса

Рейтинг статьи

0 комментариев

Старые

Новые Популярные

Межтекстовые Отзывы

Посмотреть все комментарии