Пример №7 из задания 12

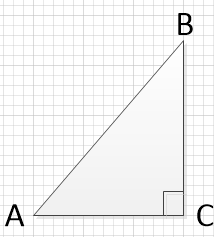
В треугольнике $ABC$ угол $C$ равен $90^{\circ}$ , $AB = 3\sqrt{5}$ , $\displaystyle sinA=\frac{2}{\sqrt{5}}$ . Найдите площадь треугольника.

Решение

Синус – отношение противолежащего катета к гипотенузе, т.е. $\displaystyle sinA=\frac{BC}{AB}$ . Подставим известные значения и найдем катет $BC$ :

$\displaystyle \frac{2}{\sqrt{5}}=\frac{BC}{3\sqrt{5}};$

$BC=6$ .

Косинус – отношение прилежащего катета к гипотенуз, т.е. $\displaystyle cosA=\frac{AC}{AB}$ . Найдем $cosA$ , для этого воспользуемся основным тригонометрическим тождеством $sin^2x+cos^2x=1$ :

$\displaystyle \frac{4}{5}+cos^2A=1;$

$\displaystyle cosA=\frac{1}{\sqrt{5}}$ .

Подставим известные значения и найдем катет $AC$ :

$\displaystyle \frac{1}{\sqrt{5}}=\frac{AC}{3\sqrt{5}};$

$AC=3$ .

Площадь прямоугольного треугольника находится по формул $\displaystyle S=\frac{a\cdot b}{2}$ , где $a$ и $b$ – катеты треугольника. Подставим известные значения в формул и найдем площадь треугольника:

$S=(3\cdot 6)\div2=9$ .

Ответ: $9$ .

Источник: ЕГЭ 2023 Математика. Базовый уровень. Типовые экзаменационные варианты. 30 вариантов (вариант 8) (Купить книгу)