Пример №12 из задания 12

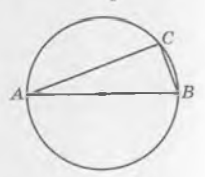
На окружности радиуса $\sqrt{10}$ отмечена точка $C$ . Отрезок $АВ$ – диаметр окружности, $АС = 6$ . Найдите $ВС$ .

Решение

Т.к. треугольник вписан в окружность, то он является прямоугольным, т.к. вписанный угол, опирающийся на диаметр, прямой.

Диаметр окружности равен $2\cdot \sqrt{10}=2\sqrt{10}$ .

Значит, можно найти $BC$ по теореме Пифагора:

$AB^2=AC^2+BC^2;$

$40=36+BC^2;$

$BC=2$ .

Ответ: $2$ .

Источник: ЕГЭ 2023 Математика. Базовый уровень. Типовые экзаменационные варианты. 30 вариантов (вариант 13) (Купить книгу)

0 0 голоса

Рейтинг статьи

0 комментариев

Старые

Новые Популярные

Межтекстовые Отзывы

Посмотреть все комментарии