Пример №17 из задания 13
Радиус основания цилиндра равен 15, а его образующая равна 14. Сечение, параллельное оси цилиндра, удалено от неё на расстояние, равное 9. Найдите площадь этого сечения.
Решение
Сечение является прямоугольником. По условию, мы знаем одну сторону прямоугольника и оно равняется 14. Найдем вторую сторону прямоугольника. Для этого, из прямоугольного треугольника ABC найдем катет AC по теореме Пифагора:
BC^2=AB^2+AC^2;
15^2=9^2+AC^2;
AC=12.
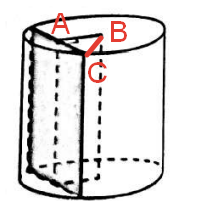
А целая сторона прямоугольника равняется AC \cdot 2=12\cdot 2=24.
Обе стороны прямоугольника известны, значит, можно найти его площадь S=24\cdot 14=336.
Ответ: 336.
Источник: ЕГЭ 2023 Математика. Базовый уровень. Типовые экзаменационные варианты. 30 вариантов (вариант 18) (Купить книгу)
Подписаться
авторизуйтесь
0 комментариев
Старые
Задай вопрос









