Пример №20 из задания 13
Через точку, делящую высоту конуса в отношении 1:2, считая от вершины, проведена плоскость, параллельная основанию. Найдите объём этого конуса, если объём конуса, отсекаемого от данного конуса проведённой плоскостью, равен 20.
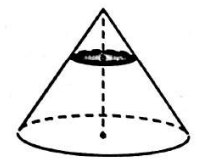
Решение
Конус разделен на 1+2=3 части. Высота меньшего конуса равна \displaystyle \frac{1}{3} высота всего конуса.
Объемы подобных тел относятся как куб коэффициента подобия, значит, объем большего конуса в 3^3=27 раз больше объема меньшего конуса.
Нам известен объем маленького конуса, значит, можно найти и объем большего конуса и он равен 27\cdot 20=540.
Ответ: 540.
Источник: ЕГЭ 2023 Математика. Базовый уровень. Типовые экзаменационные варианты. 30 вариантов (вариант 22) (Купить книгу)
Подготовка к ОГЭ по математике - что нужно знать школьнику
Алгебра в жизни - 7 примеров, где тебе пригодятся школьные знания
Готовимся к контрольной - план на неделю для 7–9 классов
Интерактивные способы учить математику - сайты, приложения, игры
5 распространённых ошибок в решении уравнений и как их избежать
Почему важно задавать вопросы - как не бояться спрашивать на уроке
Подписаться
авторизуйтесь
0 комментариев
Старые
