Пример №37 из задания 1

Треугольник $ABC$ вписан в окружность с центром $O$ . Угол $BAC$ равен $32 ^{\circ}$ . Найдите угол $BOC$ . Ответ дайте в градусах.

Решение

Изобразим условие:

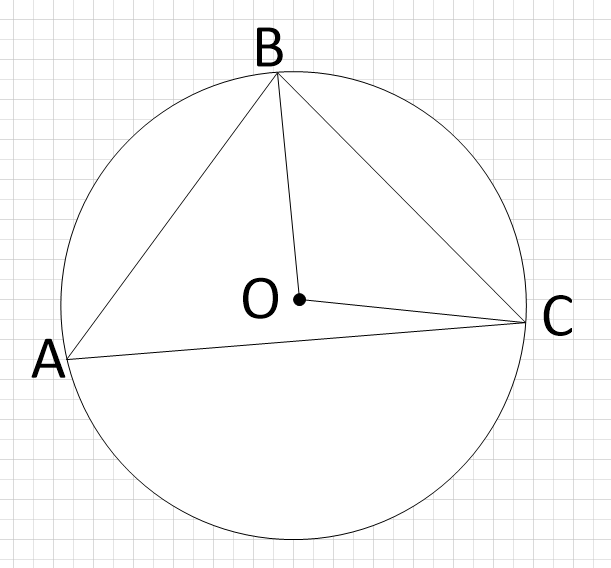
Теорема о вписанном угле гласит: вписанный угол равен половине центрального угла, опирающегося на ту же дугу, т.е.:

$\displaystyle \angle BAC=\frac{\angle BOC}{2};$

$\displaystyle \angle BOC=\angle BAC \cdot 2;$

$\angle BOC=32 \cdot2=64^{\circ}$ .

Получилось, что угол $BOC$ равен $64^{\circ}$ .

Ответ: $64$ .

Источник: Демоверсия ЕГЭ по математике 2024. Профильный уровень (Задание 1. Пример 1)

0 0 голоса

Рейтинг статьи

0 комментариев

Старые

Новые Популярные

Межтекстовые Отзывы

Посмотреть все комментарии