Пример №38 из задания 1

Площадь треугольника $ABC$ равна $24$ ; $DE$ – средняя линия, параллельная стороне $AB$ . Найдите площадь треугольника $CDE$ .

Решение

Изобразим условие:

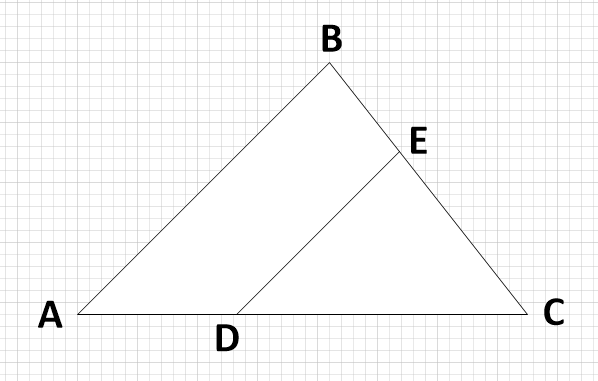
Средняя линия треугольника отсекает о него треугольник, подобный данному с коэффициентом $\displaystyle \frac{1}{2}$ . Т.е. в нашем случае треугольник $DEC$ подобен треугольнику $ABC$ с коэффициентом $\displaystyle \frac{1}{2}$ .

Площади подобных треугольников относятся как квадрат коэффициента подобия. т.е. $\displaystyle \frac{\bigtriangleup CDE}{\bigtriangleup ABC}=\left( \frac{1}{2}\right)^2=\frac{1}{4}$ .

Отсюда можно найти площадь треугольника $CDE$ :

$\displaystyle CDE=\frac{24}{4}=6$ .

Ответ: $6$ .

Источник: Демоверсия ЕГЭ по математике 2024. Профильный уровень (Задание 1. Пример 2)