Пример №40 из задания 1

Стороны параллелограмма равны 24 и 27. Высота, опущенная на меньшую из этих сторон, равна 18. Найдите высоту, опущенную на большую сторону параллелограмма.

Решение

Изобразим условие:

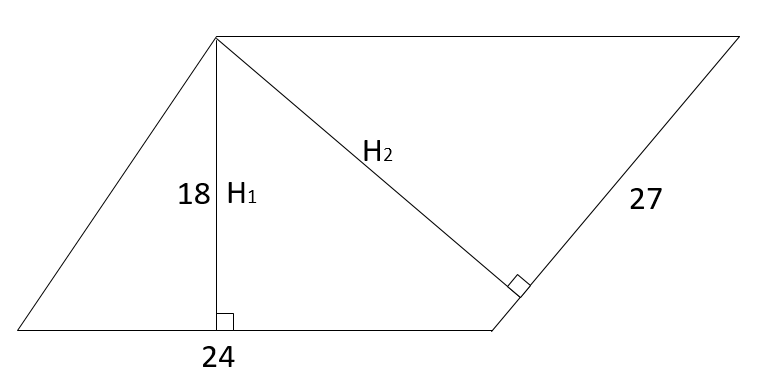
Площадь параллелограмма можно найти по формуле $S=a \cdot h$ , где $a$ – основание, $h$ – высота.

В нашем случае площадь можно найти двумя способам. Первый – используя высоту $h_1$ и меньшую сторону (основание) $24$ . Второй – используя высоту $h_2$ и большую сторону (основание) $27$ .

Найдем площадь первым способом $S=a_1 \cdot h_1=24 \cdot 18=432$ .

Зная площадь, можно найти высоту, опущенную на большую сторону параллелограмма:

$S=a_2 \cdot h_2;$

$432=27 \cdot h_2;$

$h_2=16$ .

Получилось, что высота, опущенная на большую сторону параллелограмма равна $16$ .

Ответ: $16$ .

Источник: Демоверсия ЕГЭ по математике 2024. Профильный уровень (Задание 1. Пример 4)