Пример №1 из задания 7

Найдите $\sin2 \alpha$ , если $\cos \alpha=0,6$ и $\pi<\alpha<2\pi$ .

Решение

Применим основное тригонометрическое тождество $\sin^2 \alpha + \cos^2 \alpha=1$ :

$\sin^2 \alpha + 0,6^2=1;$

$\sin^2 \alpha+0,36=1;$

$\sin^2 \alpha=1-0,36;$

$\sin^2 \alpha=0,64;$

$\sin \alpha=\pm 0,8$ .

У нас известно, что $\pi<\alpha<2\pi$ . А это $3$ и $4$ четверти. Синус в этих четвертях имеет отрицательное значение, значит, $\sin \alpha=-0,8$ .

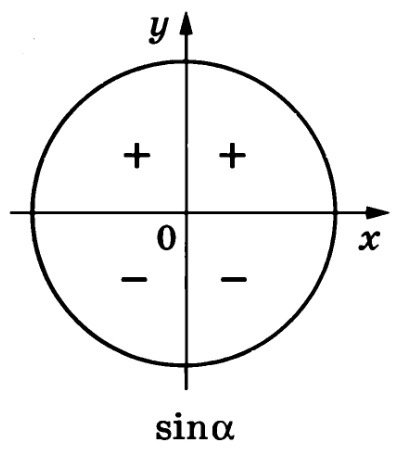
Применим формулу двойного угла $\sin 2 \alpha=2\sin \alpha \cdot \cos \alpha$ :

$\sin 2 \alpha=2 \cdot (-0,8) \cdot 0,6=-0,96$ .

Ответ: $-0,96$ .

Источник: Демоверсия ЕГЭ по математике 2024. Профильный уровень (Задание 7. Пример 1)

0 0 голоса

Рейтинг статьи

0 комментариев

Старые

Новые Популярные

Межтекстовые Отзывы

Посмотреть все комментарии