Пример №1 из задания 7

На рисунке изображены график функции и касательные, проведённые к нему в точках с абсциссами A, B, C и D.

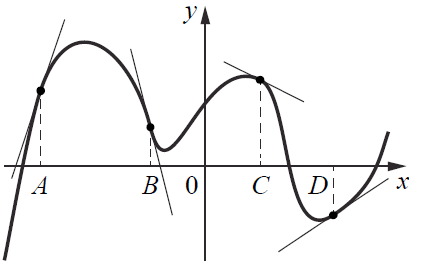
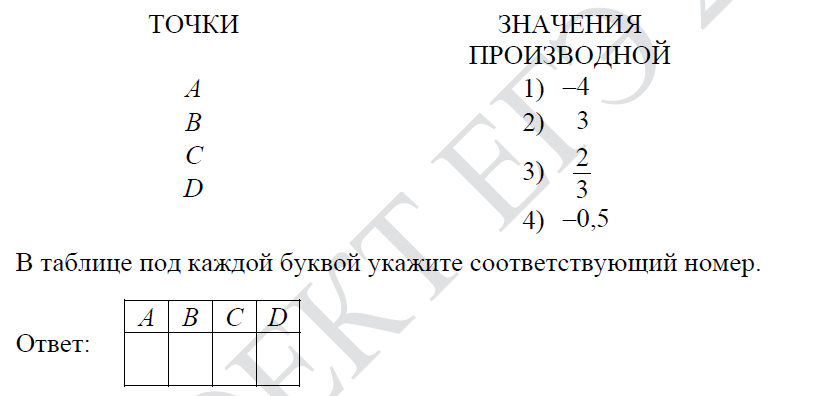
В правом столбце указаны значения производной функции в точках A, B, C и D. Пользуясь графиком, поставьте в соответствие каждой точке значение производной функции в ней.

Решение

Значение производной функции в точке равно угловому коэффициенту касательной. При этом, если касательная образует острый угол с осью $x$ , то ее значение положительное. Если образует тупой угол, то ее значение отрицательное. И чем больше угол касательное, тем большее значение принимает производная.

Касательные имеют острые углы у точек $A$ и $D$ , значит, их значение положительное. При этом, угол у точки $A$ возрастает быстрее, чем у точки $D$ , значит у $A$ значение производной большее. Соответственно, у $A$ значение равно $3$ , у $D$ значение равно $\displaystyle \frac{2}{3}$ .

Касательные имеют тупые углы у точек $B$ и $C$ , значит, их значение отрицательные. При этом, угол у точки $B$ убывает быстрее, чем у точки $C$ , значит у $B$ значение производной большее. Соответственно, у $B$ значение равно $-4$ , у $C$ значение равно $-0,5$ .

В итоге, получилась следующая последовательность $2, 1, 4, 3$ .

Ответ: $2, 1, 4, 3$ .

Источник: Демоверсия ЕГЭ по математике 2024. Базовый уровень (Задание 7. Пример 1)