Пример №1 из задания 22

Постройте график функции $\displaystyle y=\frac{x^4-13x^2+36}{(x-3)(x+2)}$ и определите, при каких значениях $c$ прямая $y=c$ имеет с графиком ровно одну общую точку.

Решение

ОДЗ:

$x-3 \neq 0$ отсюда $x \neq 3$ .

$x+2 \neq 0$ отсюда $x \neq -2$ .

Разложим числитель на множители:

$x^4-13x^2+36=0;$

Пусть $t=x^2$ :

$t^2-13t+36;$

$D=b^2-4ac=169-4 \cdot 1 \cdot 36=25;$

$\displaystyle x_1=\frac{-b+\sqrt{D}}{2a}=\frac{13+5}{2}=9;$

$\displaystyle x_2=\frac{-b-\sqrt{D}}{2a}=\frac{13-5}{2}=4.$

Соответственно $(t-4)(t-9)$ .

Заменим обратно на $x$ :

$(x^2-4)(x^2-9)$ .

Воспользуемся формулой разности квадратов $a^2-b^2=(a-b)(a+b)$ :

$(x-2)(x+2)(x-3)(x+3)$ .

$\displaystyle y=\frac{(x-2)(x+2)(x-3)(x+3)}{(x-3)(x+2)}=(x-2)(x+3)=x^2+x-6$ .

Вершина параболы:

$\displaystyle x=-\frac{b}{2a}=-\frac{1}{2}=-0,5;$

$\displaystyle y=(-0,5)^2-0,5-6=-6,25.$

Изобразим параболу.

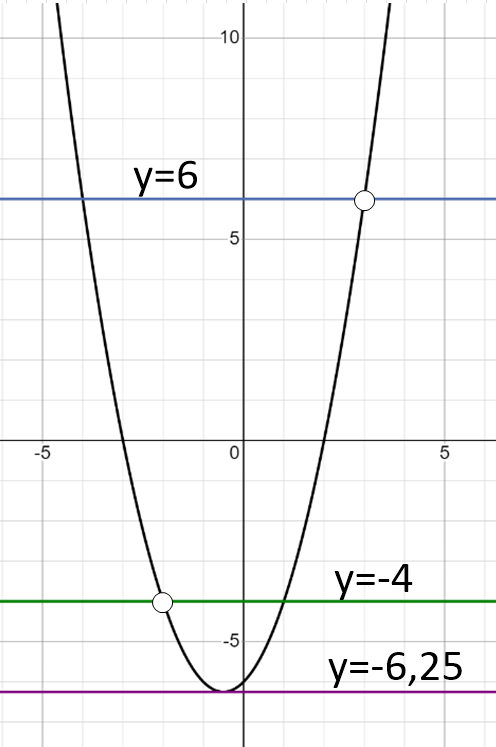
Прямая $y=c$ имеет с параболой одну общую точку когда проходит через вершину параболы или когда пересекает параболу в двух точках, одна из которых выколота. Получаем следующие значения:

$с=-6,25;$

$с=-4;$

$с=6$ .

Ответ: $c=-6,25, с=-4, c=6$ .

Источник: Решебник демоверсии ОГЭ по математике 2024 (Задание 22)