Пример №1 из задания 24

В параллелограмме ABCD точка E – середина стороны AB. Известно, что EC = ED. Докажите, что данный параллелограмм – прямоугольник.

Решение

Изобразим условие:

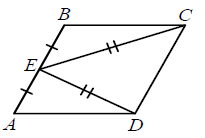
По условию $EC=ED$ и $AE=BE$ (т.к. точка $E$ – середина стороны $AB$ ). Противолежащие стороны параллелограмма равны, значит, $BC=AD$ . Получается, что треугольники $AED$ и $EBC$ равны по трем сторонам.

Значит, $\angle EAD=\angle EBC$ и их сумма равна $180^{\circ}$ . А т.к. углы равны, то и каждый угол будет равен $180 \div 2=90^{\circ}$ . Соответственно, параллелограмм с углами $90^{\circ}$ является прямоугольником.

Ответ: $5$ .

Источник: Решебник демоверсии ОГЭ по математике 2024 (Задание 24)