Пример №1 из задания 25

Основание AC равнобедренного треугольника ABC равно 12. Окружность радиусом 8 с центром вне этого треугольника касается продолжений боковых сторон треугольника и касается основания AC. Найдите радиус окружности, вписанной в треугольник ABC.

Решение

Изобразим условие:

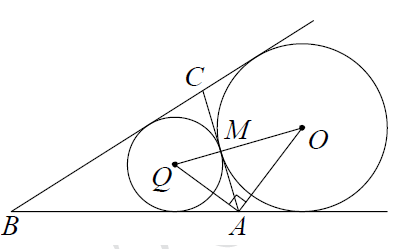
Пусть $O$ – центр вневписанной окружности, а $Q$ – центр вписанной окружности треугольника $ABC$ .

Точка касания $M$ окружностей делит $AC$ пополам (т.е. $AM=MC=AC \div 2=12 \div 2=6$ ), т.к. биссектриса треугольника делит пополам сторону, к которой она проведена.

Лучи $AQ$ и $AO$ – биссектрисы смежных углов, значит, угол $OAQ$ прямой (биссектрисы смежных углов взаимно перпендикулярны).

Квадрат высоты прямоугольного треугольника, проведённой к гипотенузе, равен произведению проекций катетов на гипотенузу. Значит, из прямоугольного треугольника $OAQ$ получаем $AM^2=MQ \cdot MO$ . Подставим известные данные:

$6^2=MQ \cdot 8;$

$36=MQ \cdot 8;$

$MQ=36 \div 8;$

$MQ=4,5$ .

Ответ: $4,5$ .

Источник: Решебник демоверсии ОГЭ по математике 2024 (Задание 25)