Пример №2 из задания 8

На рисунке изображены график функции $y=f(x)$ и касательная к нему в точке с абсциссой $x_0$ . Найдите значение производной функции $f(x)$ в точке $x_0$ .

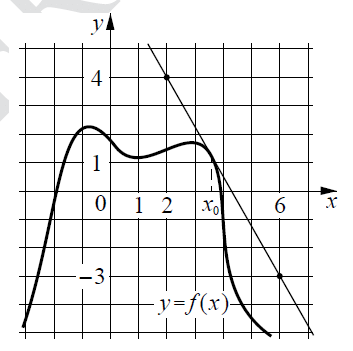
Решение

Значение производной функции в точке равно угловому коэффициенту касательной к графику функции в этой точке (тангенс угла между касательной и осью $O_x$ ).

На рисунке прямая убывает, значит, коэффициент будет отрицательным.

Построим прямоугольный треугольник:

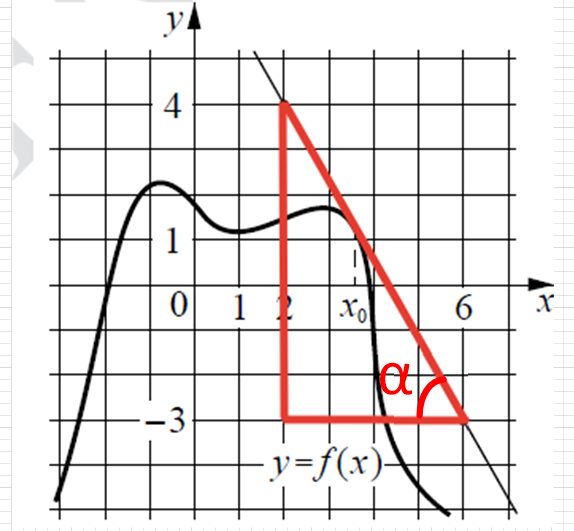
Тангенс – отношение противолежащего катета к прилежащему катету. Противолежащий катет равен $7$ клеток, прилежащий – $4$ клетки.

Значит, $\displaystyle tg \alpha = \frac{7}{4}=1,75$ .

Но выше мы прописали, что т.к. прямая убывает, то коэффициент отрицательный, значит, значение производной функции будет отрицательным и будет равняться $-1,75$ .

Ответ: $-1,75$ .

Источник: Демоверсия ЕГЭ по математике 2024. Профильный уровень (Задание 8. Пример 2)