Пример №37 из задания 11

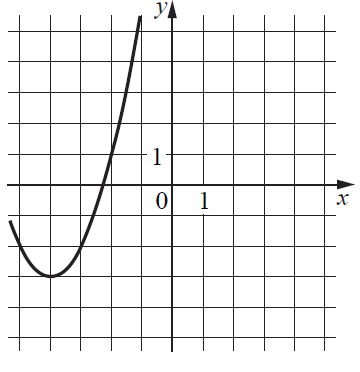
На рисунке изображён график функции вида $f(x)=ax^2+bx+c$ , где числа $a$ , $b$ и $c$ – целые. Найдите значение $f(-12)$ .

Решение

На рисунке изображена парабола с вершиной в точке $(-4;-3)$ . По графику видно, что коэффициент $a=1$ .

Координата $x$ вершин параболы находится по формуле:

$\displaystyle x=-\frac{b}{2a}$ .

Найдем отсюда коэффициент $b$ :

$\displaystyle -4=-\frac{b}{2\cdot 1};$

$-4 \cdot 2=-b;$

$b=8$ .

Найдем коэффициент $c$ :

$y=ax^2+bx+c;$

$-3=1\cdot (-4)^2+8\cdot (-4)+c;$

$-3=16-32+c;$

$c=32-16-3=13$ .

Получается, что функция имеет следующий вид $f(x)=x^2+8x+13$ .

Найдем $f(-12)$ :

$f(-12)=(-12)^2+8\cdot (-12)+13=144-96+13=61$ .

Ответ: $61$ .

Источник: Демоверсия ЕГЭ по математике 2024. Профильный уровень (Задание 11. Пример 1)

0 0 голоса

Рейтинг статьи

0 комментариев

Старые

Новые Популярные

Межтекстовые Отзывы

Посмотреть все комментарии