Пример №71 из задания 12

Найдите точку минимума функции $\displaystyle y=-\frac{x}{x^2+256}$ .

Решение

$Для нахождения производной применим следующее правило дифференцирования [latex] \displaystyle \frac{u}{v}=\frac{u’v-uv’}{v^2}:$

$\displaystyle y=-\frac{x^2+256-x\cdot 2x}{(x^2+256)^2}=\frac{x^2-256}{(x^2+256)^2} .$

Найдем точки экстремума функции, для этого приравняем производную функции к нулю:

$\displaystyle \frac{x^2-256}{(x^2+256)^2}=0.$

Знаменатель строго больше нуля. Соответственно, чтобы уравнение равнялось нулю, необходимо, чтобы числитель был равен нулю:

$x^2-256=0;$

$x=\pm 16.$

Определим знаки производной функции и изобразим на рисунке поведение функции:

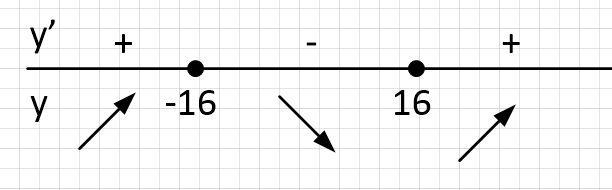
Точка минимума — точка, где производная меняет свой знак с минуса на плюс. В нашем случае точка минимума $16$ .

Ответ: $16$ .

Источник: Демоверсия ЕГЭ по математике 2024. Профильный уровень (Задание 12. Пример 3)

0 0 голоса

Рейтинг статьи

0 комментариев

Старые

Новые Популярные

Межтекстовые Отзывы

Посмотреть все комментарии