Пример №11 из задания 12

В трапеции ABCD площадь равна 27, AD = 6, BC = 3. Найдите площадь треугольника ABC.

Решение

Площадь трапеции находится по формуле S=h⋅a+b2\displaystyle S=h\cdot \frac{a+b}{2}, где aa и bb – основания трапеции, hh – высота трапеции.

Подставим все известные значения в формулу и найдем высоту трапеции:

27=6+32⋅h;\displaystyle 27=\frac{6+3}{2}\cdot h;

h=6h=6.

Достроим высоту. Высота трапеции равна высоте треугольника ABCABC.

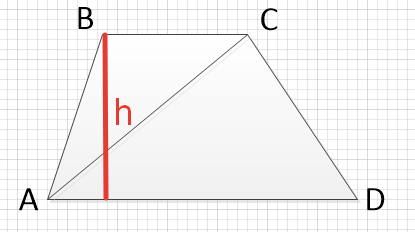
Площадь треугольника найдем по формуле S=12⋅a⋅h\displaystyle S=\frac{1}{2}\cdot a \cdot h, где aa – основание треугольника, hh – высота треугольника. Подставим известные значения в формулу и найдем площадь треугольника S=(3⋅6)÷2=9S=(3\cdot6)\div2=9.

Ответ: 99.

Источник: ЕГЭ 2023 Математика. Базовый уровень. Типовые экзаменационные варианты. 30 вариантов (вариант 12) (Купить книгу)

  • 5 распространённых ошибок в решении уравнений и как их избежать5 распространённых ошибок в решении уравнений и как их избежать
  • Готовимся к контрольной - план на неделю для 7–9 классовГотовимся к контрольной - план на неделю для 7–9 классов
  • Интерактивные способы учить математику - сайты, приложения, игрыИнтерактивные способы учить математику - сайты, приложения, игры
  • Почему важно задавать вопросы - как не бояться спрашивать на урокеПочему важно задавать вопросы - как не бояться спрашивать на уроке
  • Алгебра в жизни - 7 примеров, где тебе пригодятся школьные знанияАлгебра в жизни - 7 примеров, где тебе пригодятся школьные знания
  • Как понять геометрию - визуальные методы для запоминания теоремКак понять геометрию - визуальные методы для запоминания теорем
    • 0 0 голоса
    Рейтинг статьи
    Подписаться
    Уведомить о
    guest


    0 комментариев
    Старые
    Новые Популярные
    Межтекстовые Отзывы
    Посмотреть все комментарии
    0
    Оставьте комментарий! Напишите, что думаете по поводу статьи.x