Пример №18 из задания 20
Решите неравенство
Решение
ОДЗ:
Получилось, что и
Неравенство не может быть равно нулю, т.к. числитель не равен нулю.
Т.к. числитель отрицательное число, то неравенство будет меньше нуля, если знаменатель будет больше нуля, т.е.
Воспользуемся методом интервалов:
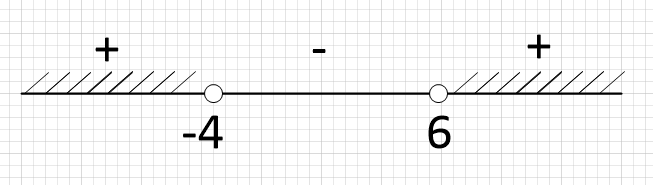
Получилось, что
Ответ:
Источник: ОГЭ-2025. Математика. Типовые экзаменационные варианты. 36 вариантов. Ященко И. В. (вариант 27)
ОГЭ-2024. Математика. Типовые экзаменационные варианты. 36 вариантов (вариант 17)
- Р Р‡.МессенРТвЂВВВВВВВВжер
- ВКонтакте
- РћРТвЂВВВВВВВВнокласснРСвЂВВВВВВВВРєРСвЂВВВВВВВВ
- Telegram
- Viber
- РњРѕР№ Р В Р’В Р РЋРЎв„ўР В Р’В Р РЋРІР‚ВВВВВВВВРЎР‚
Подписаться
авторизуйтесь
0 комментариев
Старые
Задай вопрос










