Пример №22 из задания 5

Юрий Борисович начал строить на дачном участке теплицу (рис. 1). Для этого он сделал прямоугольный фундамент длиной 6 м (DC на рис. 2) и шириной 2,4 м (AD на рис. 2). Нижний ярус теплицы имеет форму прямоугольного параллелепипеда, собран из металлического профиля и по длине для прочности укреплён металлическими стойками. Высота нижнего яруса теплицы в два раза меньше её ширины. Для верхнего яруса теплицы Юрий Борисович заказал металлические дуги в форме полуокружностей, которые крепятся к стойкам нижнего яруса. Отдельно требуется купить материал для обтяжки поверхности теплицы. В передней стенке планируется вход, показанный на рис.1 прямоугольником EFKN, где точки E, P и N делят отрезок AD на равные части. Внутри теплицы Юрий Борисович планирует сделать три грядки: одну широкую центральную и две одинаковые узкие по краям, как показано на рис. 2. Между грядками и при входе в теплицу будут дорожки шириной 40 см, для которых надо купить тротуарную плитку размером 20×20 см.

Задание 5: Найдите высоту EF входа в теплицу в сантиметрах с точностью до целого.

Решение

Введем обозначения:

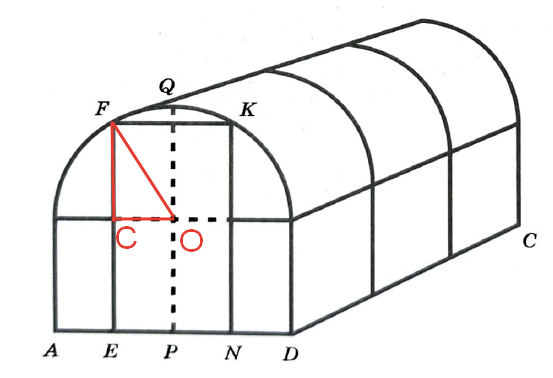
Высота равна $EF=FC+CE.$

$CE$ мы нашли из 1 задания и она равняется $CE=1,2$ м или $120$ см.

Найдем $FC$ . Для этого рассмотрим прямоугольный треугольник $FCO$ . В нем известно $FO=r=1,2$ м (нашли в 1 задании). Сторона $CO=AD \div 4=2,4 \div 4=0,6$ м или $60$ см, т.к. в передней стенке планируется вход, показанный на рис.1 прямоугольником EFKN, где точки E, P и N делят отрезок AD на равные части. Найдем $FC$ по теореме Пифагора:

$FO^2=FC^2+CO^2;$

$120^2=FC^2+60^2;$

$14400=FC^2+3600;$

$FC^2=10800;$

$FC=\sqrt{10800}$ см.

Найдем высоту $EF:$

$EF=FC+CE=\sqrt{10800} + 120=\sqrt{100 \cdot 108} + 120=10\sqrt{108} + 120=10\sqrt{9 \cdot 12} + 120=30\sqrt{12} + 120=30\sqrt{4 \cdot 3} + 120=60\sqrt{3}+120 \approx 60 \cdot 1,73 + 120 \approx 223,8 \approx 224$ см.

Ответ: $224$ .,

Источник: ОГЭ-2025. Математика. Типовые экзаменационные варианты. 36 вариантов. Ященко И. В. (вариант 21)