Пример №24 из задания 5
Роман Михайлович начал строить на дачном участке теплицу длинной 4,4 метров (DC на рис. 1). Для этого он сделал прямоугольный фундамент (рис. 2). Для каркаса теплицы нужно заказать металлические дуги в форме полуокружностей длиной 5 м каждая и покрытие для обтяжки теплицы. Отдельно требуется купить плёнку для передней и задней стенок теплицы. В передней стенке планируется вход, показанный на рис. 1 прямоугольником ЕFКN, где точки Е, Р и N делят отрезок АD на равные части. Внутри теплицы Роман Михайлович планирует сделать три грядки, как показано на рис. 2. Между грядками и при входе в теплицу будут дорожки шириной 40 см, для которых надо купить тротуарную плитку размером 20×20 см.
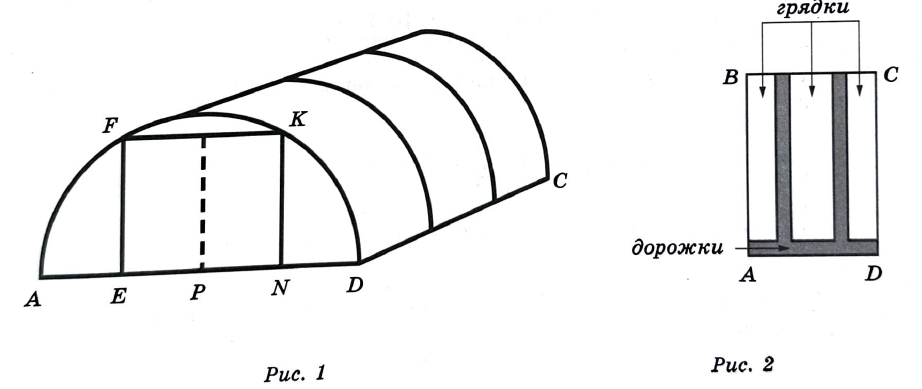
Задание 5: Найдите высоту EF входа в теплицу в сантиметрах с точностью до целого.
Решение
По условию, в передней стенке планируется вход, показанный на рис. 1 прямоугольником ЕFКN, где точки Е, Р и N делят отрезок АD на равные части. Мы знаем ширину AD=3,2 м (нашли из задания 2). Значит AE=EP=PN=ND=3,2 \div 4=0,8 м.
\displaystyle PF=AP=r=AE+EP=0,8+0,8=1,6 м.
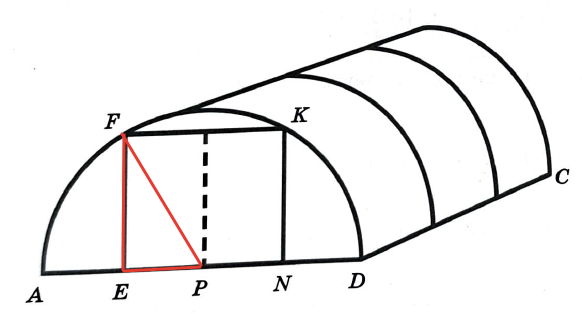
Найдем высоту EF из прямоугольного треугольника FEP по теореме Пифагора:
FP^2=FE^2+EP^2;
160^2=FE^2+80^2;
25600=EF^2+6400;
EF^2=19200;
EF=\sqrt{19200}.
Корень квадратный находится между числами 138^2=19044 и 139^2=19321.
Запишем в ответ число 139.
Ответ: 139.
Источник: ОГЭ-2024. Математика. Типовые экзаменационные варианты. 36 вариантов (вариант 35)









