Пример №42 из задания 3
Иван Викторович решил построить на дачном участке теплицу длиной 4,2 метров. Для этого он сделал прямоугольный фундамент. Для каркаса теплицы Иван Викторович заказывает металлические дуги в форме полуокружностей длиной 4,71 м каждая и пленку для обтяжки. Отдельно требуется купить плёнку для передней и задней стенок теплицы. В передней стенке планируется вход, показанный на рисунке прямоугольником АСDB. Точки А и В — соответственно середины отрезков МО и ОN.
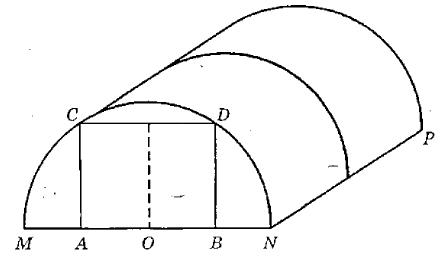
Задание 3: Найдите примерную площадь участка внутри теплицы в квадратных метрах. Число π возьмите равным 3,14.
Решение
Участок внутри теплицы имеет форму прямоугольника, площадь которого можно найти по формуле:
S= a \cdot b.
Длина a известно из условия, она равна 4,2 м. А ширину b=MN мы нашли в задании 2 и она равна 3 м.
Подставим известные значения в формулу и найдем площадь прямоугольника:
S=4,2 \cdot 3 = 12,6 кв. м.
Получается, что площадь участка внутри теплицы равна 12,6 кв. м.
Ответ: 12,6.
Источник: ОГЭ 2025. Математика. 50 вариантов. Типовые варианты экзаменационных заданий от разработчиков ОГЭ. Ященко И. В. (вариант 6)
Готовимся к контрольной - план на неделю для 7–9 классов
Почему важно задавать вопросы - как не бояться спрашивать на уроке
Квадратные уравнения. Решение квадратных уравнений. Дискриминант. Формула дискриминанта. Примеры.
Алгебра в жизни - 7 примеров, где тебе пригодятся школьные знания
Интерактивные способы учить математику - сайты, приложения, игры
Подготовка к ОГЭ по математике - что нужно знать школьнику
Подписаться
авторизуйтесь
0 комментариев
Старые
