Пример №42 из задания 4
Иван Викторович решил построить на дачном участке теплицу длиной 4,2 метров. Для этого он сделал прямоугольный фундамент. Для каркаса теплицы Иван Викторович заказывает металлические дуги в форме полуокружностей длиной 4,71 м каждая и пленку для обтяжки. Отдельно требуется купить плёнку для передней и задней стенок теплицы. В передней стенке планируется вход, показанный на рисунке прямоугольником АСDB. Точки А и В — соответственно середины отрезков МО и ОN.
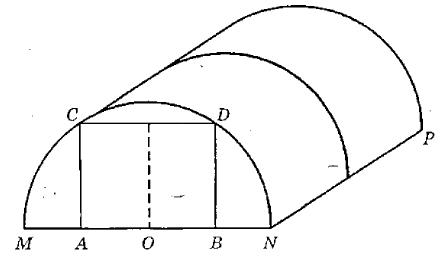
Задание 4: Сколько квадратных метров плёнки нужно купить для передней и задней стенок, если в учётом крепежа её нужно покупать с запасом 10%? Число π возьмите равным 3,14. Результат округлите до десятых.
Решение
Задняя и передняя стеки в виде полукруга. Их общая площадь будет равна площади круга, которую можно найти по формуле:
S=\pi \cdot R^2.
Найдем чему равен радиус:
R=MN \div 2 = 3 \div 2 = 1,5 м. (из задания 2)
Найдем площадь круга:
S=3,14 \cdot 1,5^2=7,065 кв. м.
Запас плёнки должен составлять 7,065 \div 100 \cdot 10=0,7065 кв. м.
В итоге необходимо купить 7,065+0,7065=7,7715\approx 7,8 кв. м. пленки.
Ответ: 7,8.
Источник: ОГЭ 2025. Математика. 50 вариантов. Типовые варианты экзаменационных заданий от разработчиков ОГЭ. Ященко И. В. (вариант 6)
5 распространённых ошибок в решении уравнений и как их избежать
Подготовка к ОГЭ по математике - что нужно знать школьнику
Почему важно задавать вопросы - как не бояться спрашивать на уроке
Готовимся к контрольной - план на неделю для 7–9 классов
Как понять геометрию - визуальные методы для запоминания теорем
Квадратные уравнения. Решение квадратных уравнений. Дискриминант. Формула дискриминанта. Примеры.
Подписаться
авторизуйтесь
0 комментариев
Старые
