Пример №7 из задания 4

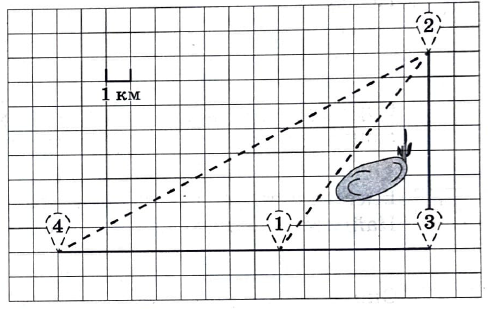
Никита и папа летом живут в деревне Лягушкино. В субботу они собираются съездить на велосипедах в село Вятское в спортивный магазин. Из деревни Лягушкино в село Вятское можно проехать по прямой лесной дорожке. Есть более длинный путь: по прямолинейному шоссе через деревню Куровка до деревни Марусино, где нужно повернуть под прямым углом налево на другое шоссе, ведущее в село Вятское. Есть и третий маршрут: в деревне Куровка можно свернуть на прямую тропинку в село Вятское, которая идет мимо пруда.

Лесная дорожка и тропинка образуют с шоссе прямоугольные треугольники.

По шоссе Никита с папой едут со скоростью 25 км/ч, а по лесной дорожке и тропинке  – со скоростью 15 км/ч. На плане изображено взаимное расположение населенных пунктов, длина стороны каждой клетки равна 1 км.

Задание 4: Сколько минут затратят на дорогу из деревни Лягушкино в село Вятское Никита с папой, если поедут через деревню Марусино?

Решение

Из задания 1 мы нашли, что деревня Марусино имеет номер $3$ , село Вятское – номер $2$ и деревня Куровка – номер $1$ . Значит, деревня Лягушкино имеет номер $4$ .

Нарисуем путь, который проедут Никита с папой:

Из точки $4$ в точку $3$ Никита с папой передвигаются по шоссе, где их скорость передвижения составляет $25$ км/ч. А из точки $3$ до точки $2$ они так же едут по шоссе, где их скорость составляет так же $25$ км/ч.

Время можно найти по формуле $\displaystyle t=\frac{S}{V}$ , где $t$ – время, $S$ – путь, $V$ – скорость.

Расстояние от точки $4$ до точки $3$ составляет $15 \cdot 1=15$ км. И скорость по шоссе $25$ км/ч. Найдем время, которое потратили Никита с папой передвигаясь от точки $4$ к точке $3$ :

$\displaystyle t_1=\frac{S}{V}=\frac{15}{25}=\frac{3}{5}$ часа.

Расстояние от точки $3$ до точки $2$ составляет $8 \cdot 1=8$ км. И скорость по шоссе $25$ км/ч. Найдем время, которое потратили Никита с папой передвигаясь от точки $3$ к точке $2$ :

$\displaystyle t_2=\frac{S}{V}=\frac{8}{25}$ часа.

Найдем общее время:

$\displaystyle t_1+t+2=\frac{3}{5}+\frac{8}{25}=\frac{3 \cdot 5+8}{25}=\frac{15+8}{25}=\frac{23}{25}$ часа.

Переведем время в минуты ( $1$ час равен $60$ минут):

$\displaystyle \frac{23}{25} \cdot 60= \frac{23}{5} \cdot 12=\frac{276}{5}=55,2$ минуты.

Ответ: $55,2$ .

Источник: ОГЭ-2024. Математика. Типовые экзаменационные варианты. 36 вариантов (вариант 4)